If you are going to research Druids and Calendars it will not be very long before you come across the Coligny Calendar. This engraved bronze tablet was discovered in 1897 in Coligny France, once the home of the Sequini tribe and for this reason it is also known as the Sequini Calendar. A similar calendar was found in nearby Villards d’Heria but only 8 small fragments of that one remained. The Coligny Calendar is the most important evidence we have for a calendar of the Celtic tribes, and therefor the ancient Druids.
When I first started the Druidcraft Calendar project, the Coligny Calendar was one of the primary inspirations along with Stonehenge. And it was the fact that both are capable of tracking the Metonic Cycle that lead me to base the Druidcraft Calendar on these systems. But the fact that the Coligny Calendar can follow a Metonic cycle is not immediately apparent. In this article I would like to clear that up, and place the Colignay Calendar firmly in it’s place as an important source of inspiration on my work.
The Bronze calendar tablet it’s self was originally 4 ft 10 in wide, 2 ft 11 tall and was written in the Gaulish language using Latin letters and numbers, and is believed to date from around the end of the 2nd Century AD.
So what is the Problem?
As discussed many times before on this site, a Metonic cycle consists of 19 solar years of 235 lunar months. Yet the Coligny Calendar is made up of only 16 columns with 62 months across 5 years. If this is the case, how can the Coligny Calendar be said to be Metonic? Since the discovery of the calendar there have been two key contentious issues with our understanding of it.
The first issue is the beginning of the year. At what point in the solar cycle should this calendar begin counting? There have been many suggestions for this, usually using our understanding of the month names as a basis. Specifically the Month “Samon” and the word Samhain both seem to share the same root of *samo- meaning “summer”. Most suggestions for the “celtic new year” then use this understanding to make their case. Suggestions usually include the Summer Solstice, the Autumn Equinox, Samhain or the Winter Solstice.
The second point of contention is whether or not the Coligny calendar is part of a wider cycle. It is possible that the calendar represents 5 specific years, and that once this period of time had passed, a new tablet would have to be produced for the next period of time. Alternatively it is possible that the tablet was used cyclically. The debate over whether it represents part of a 19 (Metonic), 25 or 30 (multiples of 5) year cycle rages on. That said, as of time of writing, if you read the wikipedia entry on the Coligny Calendar, you will find no reference to the Metonic cycle.
A closer look
The first thing to note is that the Coligny Calendar is most certainly a luni-solar calendar in that it tracks the cycles of both the moon and sun, and attempts to reconcile them over time. To achieve this, the calendar uses alternating months of 29 and 30 days, with the inclusion of additional 30 day leap months, and rules to make additional months 30 days long to catch up when the error grew to large. This is also a property of a Metonic Calendar, and the Druidcraft calendar is no different in that regard.
Further to this the Coligny calendar uses 12 lunar months per year, with the inclusion of a leap month every two and a half years. Again this is also a property of a Metonic calendar. The Coligny calendar includes these additional months every 2 and a half years. The Druidcraft calendar on the other hand includes the additional months at the point in the year where there a four new moons in a season rather than the usual three. Either way the result is the same, and every so often there is a year with 13 months. It can be said with some certainty that the calendar attempts to reconcile the moon and sun. This is our first clue that the calendar may be Metonic.

First, you need to understand how the calendar was reconstructed. Based on the fact that the calendar contains a number of repeating patterns, the gaps can be filled out with quite a lot of certainty. But when you finish this process you are left with 3 months out of the 62 on the calendar for which we do not know the length. The first issue is the intercalery month at the very beginning of the calendar is missing, the second issue is the length of the month EQUOS. Throughout the calendar, Months are marked as either MAT or ANM, which seems to indicate that a month should be 30 days (MAT) or 29 days (ANM) long. EQUOS is marked as an ANM month. Other patterns in the calendar also treat it as an ANM month. But in years 1 and 5 it has 30 days. We also have the fragment that shows the total length of the 3rd year, so we know EQUOS has 30 days in year 3 as well. The question is, how many days has EQUOS in years 2 and 4 given that all other months marked ANM are 29 days, and all other instances of EQUOS are 30 days?
The proposed solutions to these problems have been the topic of much debate, with the open question of how this calendar could possibly accurately track lunations right at the centre of it. The most popular proposals (including the one on wikipedia) have one of 2 issues. Either the proposed number of days allows the moon and sun to slip out of sync with the calendar by several days over the 5 year period. Or, in order to keep in sync with the sun and moon, two months of 28 days is used which is attested no where on any surviving fragments, and disrupts what would otherwise appear to be a thing of pure mathematical genius. I for one believe there is a better solution that maintains the symmetry and beauty of the calendar and also stays true to the actual cycles of the sun and moon. Otherwise, why go to all the effort?
The case for the 30 year cycle
The idea that the calendar might be part of 30 year cycle was first put forward by De Ricci in 1898. It was recorded by Pliny the Elder that the Gauls considered 30 years to be an age. The Calendar being 5 years long, it could be repeated 6 times to represent such a 30 year age.
Lets start with the assumption that it is important to stay in sync with the lunation cycles, and that the Coligny calendar was intended to do so. In this case we know that the average lunation takes 29.53 days, and that the calendar contains 62 months (5 years). 62 x 29.53 equals 1830.94 days. So we need the calendar to contain 1831 days.
The information on wikipedia is based on the work of Garrett Olsted and those who came before him. The number of days per month that comes closest to matching lunations from Olsted’s work is given below.
| Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
| intercal1 | 30 | ||||
| SAMON | 30 | 30 | 30 | 30 | 30 |
| DUMAN | 29 | 29 | 29 | 29 | 29 |
| RIUR | 30 | 30 | 30 | 30 | 30 |
| ANAG | 29 | 29 | 29 | 29 | 29 |
| OGRON | 30 | 30 | 30 | 30 | 30 |
| CUTIOS | 30 | 30 | 30 | 30 | 30 |
| intercal2 | 30 | ||||
| GIAMON | 29 | 29 | 29 | 29 | 29 |
| SIMUIS | 30 | 30 | 30 | 30 | 30 |
| EQUOS | 30 | 28 | 30 | 29 | 30 |
| ELEMB | 29 | 29 | 29 | 29 | 29 |
| AEDR | 30 | 30 | 30 | 30 | 30 |
| CANTL | 29 | 29 | 29 | 29 | 29 |
The number of days in this proposed solution totals 1832 days, which is one day too many. For this reason MacNeill suggests 28 days for EQUOS in year 4, reducing the total to the correct number of 1831 days.
The question is how well does this pattern match the actual lunations of the moon? Lets take a look at Olsted’s proposal as that remains the basis for most information circulating on the Coligny calendar.
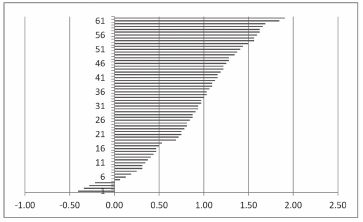
As you can see from the chart above, the calendar is almost entirely running ahead of the actual lunations of the moon, sometimes by almost 2 days. If you remove a day to bring the calendar to 1831 days then this discrepancy only gets worse. To resolve this De Ricci proposed the theory that the calendar must allow going out of sync with the sun and the moon and that it could be corrected for by removing a month every 30 years, and that over time, this could have been reduced to 25 years. Thus the proposal that the Coligny calendar follows a 30 or 25 year cycle. And it would seem from historic references that there was indeed a recognised 30 year cycle. The problem here really is not whether or not there was a historic 30 year cycle, but rather the reconstructed accuracy of the calendar that leads to that conclusion. Luckily other researchers of the Coligny Calendar such as Helen McKay have offed alternative interpretations of the unknown month lengths that lead to a more accurate tracking of the lunation cycles, which in turn makes the calendar Metonic as a Metonic calendar naturally arises from observations of the sun and moon. Let us then turn our attention back to the length of the unknown months.
Fixing the month lengths
To keep in close(ish) sync with the moon, EQUOS year 4 seems to require 29 days, resulting in 1832 days (one to many). Reducing this to 28 days gives you the correct total number, but slipping considerably against the movements of the moon in year 4. The use of 28 days is also not attested anywhere on the remaining fragments, and to be frank seems ridiculous when a system of only 30 and 29 day months can work very well. It also disrupts somewhat the beauty and balance in the calendar that seems to be such an important thing at every level, with days, months, years and even the 5 year cycle all divided up into balanced light and dark halves. So why then would they have used 28 days like that. These people were supposed to be the inheritors of the astronomical tradition of western Europe stretching right back to the Neolithic and monuments such as Stonehenge. Are we to believe they settled for such a glaring interruption to an otherwise beautiful expression of balance?
So what can we do to correct this? As already stated there is another month for which we do not know the length. The intercalary month at the very beginning of the calendar. Olsted has it at 30 days long, immediately followed by SAMON which is also 30 days long. If we need to shed a day, why not from this intercalary month rather than reducing EQUOS from 29 to 28 days in the 4th year? It is difficult to say for certain how many days the first Intercalary month has. Firstly, the notation for a 30 day month is usually MAT, but this first intercalary months has the notation of MATV and the notation is on the next line down from where it appears for other months. As we have seen with EQUOS the ANM notation may not always indicate a 29 day month anyway. Another reason is that the second intercalary month has 30 days, so the first one may have too.
There is convention in the notation that may suggest that intercalary month one was 29 days. Each day’s notation is copied from a particular other month and day. In the case of this day the notation would be copied from CANTL 30, which doesn’t exist because CANTL only has 29 days. The strongest evidence that the first intercalary month is only 29 days comes from observation. If it were 30 days long, then after only 7 months the calendar would already be more than one and a half days ahead of the moon.
If we accept the first month is 29 days, then there is only one more theory we need to look at in order to make sense of the calendar. What if EQUOS is marked ANM because it would normally have 29 days, but has 30 holes because it could be extended by a day? With this variability we can test for new solutions. And it turns out that by making the first intercalary month 29 days, as well as EQUOS in years two three and four the calendar will work very well.
| Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
| intercal1 | 29 | ||||
| SAMON | 30 | 30 | 30 | 30 | 30 |
| DUMAN | 29 | 29 | 29 | 29 | 29 |
| RIUR | 30 | 30 | 30 | 30 | 30 |
| ANAG | 29 | 29 | 29 | 29 | 29 |
| OGRON | 30 | 30 | 30 | 30 | 30 |
| CUTIOS | 30 | 30 | 30 | 30 | 30 |
| intercal2 | 30 | ||||
| GIAMON | 29 | 29 | 29 | 29 | 29 |
| SIMUIS | 30 | 30 | 30 | 30 | 30 |
| EQUOS | 30 | 29 | 29 | 29 | 30 |
| ELEMB | 29 | 29 | 29 | 29 | 29 |
| AEDR | 30 | 30 | 30 | 30 | 30 |
| CANTL | 29 | 29 | 29 | 29 | 29 |
We can of coarse check then to see how well this fits with the actual lunations of the moon.
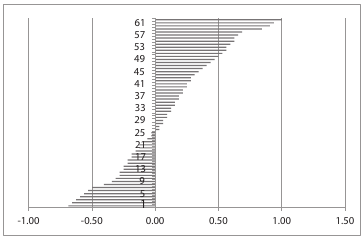
As you can see from the diagram, the calendar with the proposed changes now never goes out of step with the moon by more than 1 day which is a considerable improvement. The truth is that the average lunation of 29.53 days is just that, an average. The true period of a lunation is a complex interaction between the eccentric orbits of the sun earth and moon. It makes sense to have a calendar with a little variability built in to account for that. Marking all instances of EQUOS with 30 days but also treating it as a ANM 29 day month allows for this flexibility.
The impact of this change is impressive, and fixes a number of important issues. The calendar is now the correct number of days for 5 lunar years (1831). The calendar now also stays in sync with the moon over long periods of time. Further it can now accurately represent cycles of 5, 25 and 30 years. It maintains the internal notation and sense of balance in the calendar. And finally, because it is accurate, it can now be used to track the Metonic cycle.
In fact we now have exactly the correct number of days in year 1 that if we simply drop that, and then cycle through the calendar 4 time but retaining the first year in the subsequent cycles, the Coligny calendar will act as a perfect Metonic calendar. From there all you need to do is drop 12 months and you can measure the Soros cycle and eclipses too. It’s not a big step to also use the lunar months to track Venus and the other visible planets too.
For me this represents the mathematical genius of the Druids. The reduction of the 30 year cycle and the Metonic cycle into a mere 5 year tablet. Elegantly encapsulating all the astronomical knowledge of western Europe.
Happy New Year!
Having shown that the calendar can be used as a Metonic system, let us now see if any light can be shed on the question of when the year begins. Or to phrase the question another way, how do the lunar months line up with the solar seasons?
I stated above, there are a number of suggested solutions to the problem, all based on the attempted translation and deciphering of the textual elements of the calendar. The first issue with this is that the month names on the calendar may be abbreviated, and the effort to translate these names is ongoing. There are however, a few clues.
The first month is named SAMON, or MID SAM in the very first month of the calendar, and seems to contain the the root word *samo- meaning “summer”. This can also be found in Irish words such as Samrad and Samhain. Equally the 6th month GIAMON contains the root for “winter” which can be found in the Irish Giamred and Welsh Gaeaf. This gives us a good starting place for trying to align the months with the seasons, with most attempts placing them at either the beginning, middle or end of summer and winter respectively. The next clue is the month of OGRON which is translated as “cold month”. If this translation is correct, we can try placing SAMOS and GIAMON at different points in the year, and see how OGRON lines up.
With SAMOS at the at the Summer solstice, and GIAMON at the winter solstice, OGRON would be placed around October/November time, just as the cold begins. With SAMOS placed at Samhain around November, OGRON would be placed around May, which makes no sense at all. With SAMOS placed at the Autumn Equinox, OGRON would be placed around December, which makes more sense, but then GIAMON would be around the spring equinox as winter finishes. With SAMON placed at Beltaine, then OGRON would be placed around the Autumn Equinox at the end of summer before it really gets cold.
As you can see the problem is not really resolved with the addition of OGRON. Can the question be answers elsewhere? Well we have shown that there is a legitimate linguistic connection to other Celtic languages, so what else can we learn about the start of the year from other sources?
The 10th century Cormac’s Glossary names the month of November as Gaim which is cognate with GIAMON, and May as Cetsoman/Cetsamun which is cognate with SAMOS. And as Cú Chulaind explained to Loeg:
For two divisions were formerly on the year, namely, summer from Beltaine the first of May, and winter from Samuin to Beltaine
Further there is a sixteenth century Irish manuscript, which reads:
For this was the manner in which the Fena used to spend their time. They divided the year into two parts. During the first half, namely, from Bealtaine to Samhain, they hunted each day with their dogs; and during the second half, namely from Samhain to Bealtaine, there was not a chief or a great lord or a keeper of a house of hospitality in the whole country that had not nine of the Fena quartered on him during the winter half of the year.
The argument first put forward by Sir John Rhys in 1886, that Samhain represents the beginning of the year is by no means definitive, despite being held as the most popular view by neo-pagans today. A very good case can be made for a Beltaine start to the year, which would make a lot of sense, beginning the light half of the year then.
The Colignay calendar largely remains a mystery. Many of the notations are yet to be understood and for each question we have there are multiple suggested answers. We may never uncover all of it’s secrets, but there is one thing of which we can be certain. The ancient Gaulish Druids, or whoever else it was that came up with this system. They had very advanced knowledge of the movements of the earth sun and moon. Their mathematical prowess should continue to impress us to this day. More than just being a parapegma, as a system that could encapsulate so much information the Coligny Calendar continues to be a source of inspiration for my work on the Druidcraft Calendar to this day.

Leave a Reply
You must be logged in to post a comment.